Welcome
- Struktur titik dan vector
- Perubahan struktur titik ke vector
- Perubahan struktur vektor ke titik
- Translasi
- Scalling
- Rotasi
- Perkalian Matrik
- Komposisi Transformasi
Struktur Titik dan Vektor
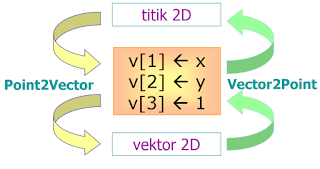
Perubahan Titik dan Vektor
Point2Vector
Fungsi ini digunakan untuk memindahkan tipe data titik
menjadi tipe data vektor. Hal ini sangat berguna untuk
operasional matrik yang digunakan dalam melakukan
transformasi dan pengolahan matrik pada grafika komputer.
Vector2Point
Fungsi ini digunakan untuk memindahkan tipe data
vektor menjadi tipe data titik. Hal ini sangat
berguna untuk penyajian grafis setelah proses
pengolahan matrik yang dikenakan pada obyek 2D.
Transformasi 2D
- Translasi
- Scaling
- Rotasi
Matrik Transformasi 2D
- Matrik transformasi adalah matrik yang membuat sebuah obyek mengalami perubahan baik berupa perubahan posisi, maupun perubahan ukuran.
- Matrik transformasi 2D dinyatakan dalam ukuran 3x3, dimana kolom ke-3 digunakan untuk menyediakan tempat untuk proses translasi.
Translasi Translasi
Translasi adalah perpindahan obyek dari titik P ke
titik P’ secara linier.
Matrik Transformasi
dari Translasi 2D
Implementasi Matrik
Tranformasi Untuk Translasi
Matrik Identitas Matrik Identitas
Scaling
Scaling m adalah perpindahan obyek dari titik P ke
titik P’, dimana jarak titik P’ adalah m kali titik P
Matrik Transformasi
dari Scaling 2D
Implementasi Matrik
Tranformasi Untuk Scaling
Rotasi
Rotasi adalah perpindahan obyek dari titik P ke titik P’,
yang berupa pemindahan berputar sebesar sudut θ
Matrik Transformasi
dari Rotasi
Implementasi Matrik
Tranformasi Untuk Rotasi
Perkalian Matrik
- Perkalian matrik dengan matrik menghasilkan matrik
- Perkalian matrik dengan vektor menghasilkan vektor
Perkalian
Matrik dengan Matrik
Perkalian matrik a dan matrik b menghasilkan
matrik c yang dirumuskan dengan
dimana i dan j bernilai 0 s/d 2
Implementasi Perkalian
Matrik dengan Matrik
Perkalian
Matrik dengan Vektor
Perkalian matrik a dan vektor b menghasilkan
vektor c yang dirumuskan dengan
dimana i bernilai 0 s/d 2
Implementasi Perkalian
Matrik dengan Vektor
Komposisi Transformasi Komposisi Transformasi
- Komposisi transformasi adalah menggabungkan beberapa tranformasi, sehingga dapat menghasilkan bentuk transformasi yang lebih kompleks
- Komposisi tranformasi dapat dilakukan dengan mengalikan matrik-matrik transformasi
Komposisi transformasi dinyatakan dengan :
Rotasi(θ).Translasi(d,0)
Contoh Komposisi Tranformasi Contoh Komposisi Tranformasi
Komposisi transformasi dinyatakan dengan :
Translasi(d,0). Rotasi(θ)
Sekian dari materi kami moga bermanfaat :) </>















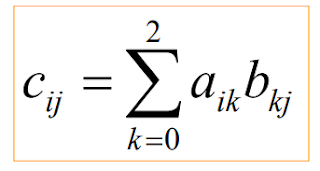









Tidak ada komentar:
Posting Komentar